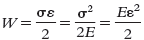Elastic Modulus (Stiffness)
An object's elastic modulus, also known as its modulus of elasticity or stiffness, is defined as its resistance to elastic deformation. The deformation is elastic if the material returns to its original shape and dimensions after the applied load (which produces extension or deflection of the sample) is removed. At low tertekan levels, this behavior happens (and therefore strains). The deformation is no longer elastic over a particular tertekan and strain, known as the elastic limit, and a permanent shape change occurs.
The elastic modulus is defined theoretically as the ratio of the rate of change of tertekan with strain for elastic stresses below the elastic limit (usually less than 0.1 percent). A material with a high stiffness is one that requires a high tertekan to produce a given strain. Elastic modulus is measured in newtons per square metre (Nm-2) or pascals in the SI system (Pa). Because many popular materials have substantial elastic modulus values, figures are frequently expressed in GPa (109 Pa).
The elastic modulus of most materials remains constant throughout a wide range of stresses (up to the elastic limit). Hooke's law applies to these materials, which are classified as linear-elastic. Non-linear elastic materials, such as rubber, are a type of non-linear elastic material. Both types of elastic behavior are depicted in the Figure 1 below. The elastic energy stored per unit volume of material is determined by the area under the stress–strain curve for any tension up to the elastic limit.
 |
| Figure 1. |
Tensile testing on a sample of the material can be used to estimate the Young's modulus. The tensile test generates data on the load created during the extension of a sample at a constant pace, as depicted in Figure 2.
 |
| Figure. 2 |
The sample is prepared with thick parts that will fit into the machine's grips and a thinner parallel section with a defined (gauge) length where the deformation will be concentrated (since the tertekan in this thinner section is larger). The engineering stress, σ , (the force causing the deformation, F, divided by the original cross-sectional area of the sample, A0) versus the engineering strain, ε , (the ratio of the extension caused by a given stress, ΔL, to the original length of the object, L0) can be plotted from load versus displacement data. The slope of the stress–strain curve (from the origin to the point where the curve deviates from linearity — this is depicted in rincian in Figure 3) can then be used to compute the Young's modulus, E. or directly using the following equation:
 |
| Figure.3 |
The area under the stress–strain curve up to this tertekan gives the work done (or elastic energy stored) per unit volume,W, as the tertekan is raised from zero to any tertekan (up to the elastic limit). Figure 3 depicts this as well. Because the Young's modulus is the stress-to-strain ratio, the energy stored can be calculated using either the applied tertekan or the applied strain. These connections are depicted as follows:
It should be noted that, due to the modest elastic stresses involved, strain measurement from the displacement of the tensile testing equipment's crosshead is frequently erroneous due to machine displacement. An extensometer (an device for measuring extension) is attached directly to the gauge length of the sample to measure the strain more precisely, and data is recorded from it.
Origin Of Properties
The'stiffness' of atom bonds can be defined in terms of the force required to extend the bond a unit distance (the'spring constant'). The bond'spring constant' divided by the length of the bond separating neighbouring atoms approximates a material's Young's modulus (or stiffness). Materials with a high ‘spring constant' and small atom separations have the highest stiffness (for small or closely packed atoms).
Because the covalent connection has a high stiffness (the spring constant is 20–200Nm-1), ceramics containing this form of bonding, such as diamond, are extremely stiff. Metallic bonding holds metals together; the spring constant of metals is 15–100Nm-1, making them stiff but not as stiff as ceramics. Rather than stretching the covalently bonded chains that tata rias the polymer's backbone, polymers deform by untangling and aligning the polymer chains in the tensile direction. Polymers have low stiffness because the connection between (rather than along) the polymer chains is weak (the spring constant is 0.5–5Nm-1).
The elastic modulus of a given material varies extremely little with alloying, heat treatment, or mechanical working because the stiffness of the links between atoms can be changed so little. The most typical method of enhancing a material's stiffness is to reinforce it with a stiffer substance, such as particles or fibres, to produce a composite.
When a material is heated, the space between atoms widens, the spring constant for the atom-atom bond shrinks, and the link between polymer chains weakens. As a result, as the temperature rises, the rigidity decreases. In fact, most materials' stiffness diminishes linearly as they approach the melting point.
Relevance To Engineering Applications
The elastic modulus is used to calculate the extension or deflection of a material under load. It works in cases where the applied force causes reversible elastic deformation rather than permanent plastic deformation. In the vast majority of engineering scenarios, this is the case, as chronic plastic deformation would result in unacceptable component distortion. The elastic modulus, for example, can be used to forecast how much a wire will stretch under tension and how much a structure, such as a beam, will deflect under load. The elastic modulus can also be used to calculate the amount of energy stored in a structure that has been elastically deformed (and so can be used to do work again), such as a spring.